Em matemática, a soma (indicada pelo grande símbolo sigma grego) é um conjunto de somas de números. Qual é a quantidade? Este é o resultado de tal ação. Se os números forem somados um após o outro da esquerda para a direita, o resultado intermediário será uma soma parcial.
Qual é o valor?
Os números a serem somados podem ser inteiros, racionais, reais ou complexos. Além deles, outros tipos de valores podem ser adicionados: vetores, matrizes, polinômios e, em geral, elementos de qualquer grupo aditivo (ou mesmo um monóide).
Se o número de elementos dos termos é finito, então a soma sempre dá um valor bem definido. A soma de uma sequência infinita de valores é chamada de série. Seu valor geralmente pode ser determinado usando um limite (embora às vezes o valor possa ser infinito).
Sequências
A soma dos números [3, 7, 2, 1] pode ser definida por uma expressão cujo valor é a soma dos dígitos incluídos nela, por exemplo 3 + 7 + 2 + 1=13. Adiçãoassociativamente, a soma não depende de como os termos são agrupados, por exemplo, (3 + 7) + (2 + 1) e 3 + ((7 + 2) + 1) ambos são iguais a nove, então os parênteses são geralmente dispensados. A adição também é comutativa, portanto, reorganizar os termos não altera o valor da soma. Observe que esta propriedade pode não funcionar para soma infinita.

Não há notação especial para somar sequências desse tipo. Há apenas uma ligeira nuance se houver menos de dois elementos. A soma de uma sequência de um membro não contém um sinal de mais (é indistinguível da forma do próprio número), e se não houver nenhum elemento, então não pode ser escrito (mas em vez disso pode ser denotado por seu valor "0"). Se, no entanto, os termos da sequência forem especificados por um padrão específico, como uma função, o operador de soma pode ser útil ou mesmo essencial.
Gravação
Para entender o que é uma soma, também é necessário analisar sua aparência.
Para somar uma sequência de números inteiros de 1 a 100, geralmente é usada uma expressão que inclui reticências para indicar os membros ausentes: 1 + 2 + 3 + 4 + … + 99 + 100. O padrão é bastante fácil de ver neste exemplo. No entanto, para opções mais complexas, é necessário especificar exatamente a regra utilizada para encontrar o valor dos elementos, o que pode ser obtido usando o operador de soma "Σ". Usando este símbolo (sigma), você pode aplicar a seguinte notação:
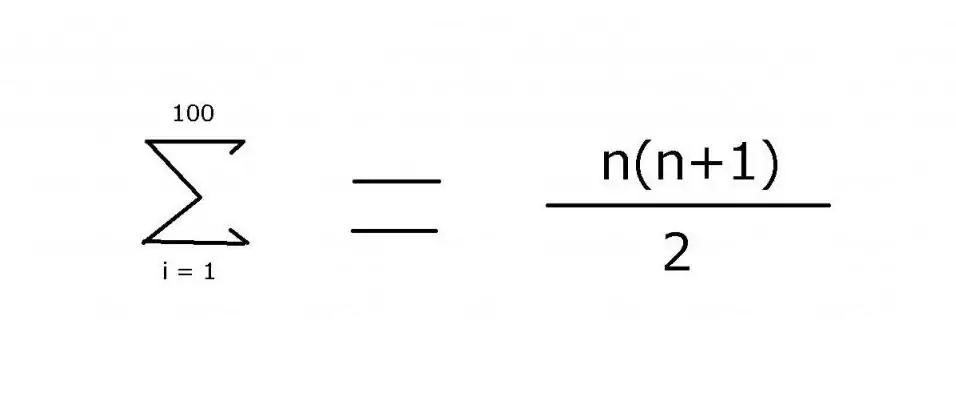
O valor desta expressão é 5050. Ele pode ser encontrado usando indução matemática, que é de onde veio a segunda parte da fórmula.
Para sequências diferentes, a fórmula mudará. O processo de gravação se reduz a buscar a pré-imagem de alguma sequência infinita e depois descrevê-la com uma fórmula. Feito isso, não é difícil entender qual é o valor em um caso específico.
Quando é necessário esclarecer que os números são somados com seus sinais (mais ou menos), utiliza-se o termo soma algébrica. Por exemplo, na teoria de circuitos elétricos, as leis de circuitos de Kirchhoff consideram a soma algébrica das correntes em uma rede de condutores que se encontram em um ponto, dando sinais opostos às correntes que entram e saem de um nó.






