Resolução é a capacidade de um sistema de imagem de reproduzir os detalhes de um objeto e depende de fatores como o tipo de iluminação usado, o tamanho do pixel do sensor e as capacidades da ótica. Quanto menor o detalhe do assunto, maior a resolução necessária da lente.
Introdução ao processo de resolução
A qualidade da imagem da câmera depende do sensor. Simplificando, um sensor de imagem digital é um chip dentro de um corpo de câmera contendo milhões de pontos sensíveis à luz. O tamanho do sensor de uma câmera determina quanta luz pode ser usada para criar uma imagem. Quanto maior o sensor, melhor a qualidade da imagem, pois mais informações são coletadas. Normalmente, as câmeras digitais anunciam no mercado tamanhos de sensor de 16 mm, Super 35 mm e, às vezes, até 65 mm.
À medida que o tamanho do sensor aumenta, a profundidade de campo diminui em uma determinada abertura, pois uma contraparte maior exige que você se aproximeobjeto ou use uma distância focal maior para preencher o quadro. Para manter a mesma profundidade de campo, o fotógrafo deve usar aberturas menores.
Essa profundidade de campo rasa pode ser desejável, especialmente para obter desfoque de fundo para retratos, mas a fotografia de paisagem requer mais profundidade, o que é mais fácil de capturar com o tamanho de abertura flexível de câmeras compactas.
Dividir o número de pixels horizontais ou verticais em um sensor indicará quanto espaço cada um ocupa em um objeto e pode ser usado para avaliar o poder de resolução da lente e resolver as preocupações do cliente sobre o tamanho do pixel da imagem digital do dispositivo. Como ponto de partida, é importante entender o que pode realmente limitar a resolução do sistema.
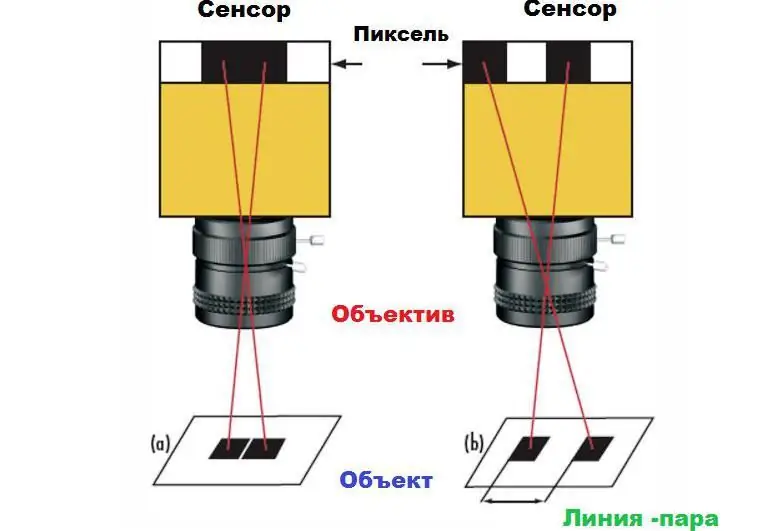
Esta afirmação pode ser demonstrada pelo exemplo de um par de quadrados em um fundo branco. Se os quadrados no sensor da câmera forem mapeados para pixels vizinhos, eles aparecerão como um grande retângulo na imagem (1a) em vez de dois quadrados separados (1b). Para distinguir os quadrados, é necessário um certo espaço entre eles, pelo menos um pixel. Esta distância mínima é a resolução máxima do sistema. O limite absoluto é determinado pelo tamanho dos pixels no sensor, bem como seu número.
Características da lente de medição
A relação entre quadrados pretos e brancos alternados é descrita como um par linear. Normalmente, a resolução é determinada pela frequência,medido em pares de linhas por milímetro - lp/mm. Infelizmente, a resolução da lente em cm não é um número absoluto. Em uma determinada resolução, a capacidade de ver os dois quadrados como objetos separados dependerá do nível da escala de cinza. Quanto maior a separação da escala de cinza entre eles e o espaço, mais estável é a capacidade de resolver esses quadrados. Essa divisão da escala de cinza é conhecida como contraste de frequência.
Frequência espacial é dada em lp/mm. Por esta razão, calcular a resolução em termos de lp/mm é extremamente útil ao comparar lentes e determinar a melhor escolha para determinados sensores e aplicações. A primeira é onde começa o cálculo da resolução do sistema. Começando com o sensor, é mais fácil determinar quais especificações de lente são necessárias para atender aos requisitos do dispositivo ou de outros aplicativos. A frequência mais alta permitida pelo sensor, Nyquist, é efetivamente dois pixels ou um par de linhas.
A resolução da lente de definição, também chamada de resolução do espaço da imagem do sistema, pode ser determinada multiplicando o tamanho em Μm por 2 para criar um par e dividindo por 1000 para converter em mm:
lp/mm=1000/ (2 X pixel)
Sensores com pixels maiores terão limites de resolução menores. Sensores com pixels menores terão melhor desempenho de acordo com a fórmula de resolução da lente acima.
Área do sensor ativo
Você pode calcular a resolução máxima para o objeto a servisualização. Para fazer isso, é necessário distinguir entre indicadores como a relação entre o tamanho do sensor, o campo de visão e o número de pixels no sensor. O tamanho deste último refere-se aos parâmetros da área ativa do sensor da câmera, geralmente determinado pelo tamanho do seu formato.
No entanto, as proporções exatas variam de acordo com a proporção, e os tamanhos nominais do sensor devem ser usados apenas como orientação, especialmente para lentes telecêntricas e grandes ampliações. O tamanho do sensor pode ser calculado diretamente a partir do tamanho do pixel e do número ativo de pixels para realizar o teste de resolução da lente.
A tabela mostra o limite de Nyquist associado aos tamanhos de pixel encontrados em alguns sensores muito usados.
| Tamanho do pixel (µm) | Limite de Nyquist acoplado (lp/mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
À medida que os tamanhos dos pixels diminuem, o limite de Nyquist associado em lp/mm aumenta proporcionalmente. Para determinar o ponto resolvível mínimo absoluto que pode ser visto em um objeto, a razão entre o campo de visão e o tamanho do sensor deve ser calculada. Isso também é conhecido como aumento primário.(PMAG).
A relação associada ao sistema PMAG permite dimensionar a resolução do espaço da imagem. Normalmente, ao projetar um aplicativo, ele não é especificado em lp/mm, mas sim em mícrons (µm) ou frações de polegada. Você pode pular rapidamente para a resolução final de um objeto usando a fórmula acima para facilitar a escolha da resolução da lente z. Também é importante ter em mente que existem muitos fatores adicionais, e a limitação acima é muito menos propensa a erros do que a complexidade de levar em conta muitos fatores e calculá-los usando equações.
Calcular distância focal
A resolução de uma imagem é o número de pixels nela. Designado em duas dimensões, por exemplo, 640X480. Os cálculos podem ser feitos separadamente para cada dimensão, mas, para simplificar, isso geralmente é reduzido a um. Para fazer medições precisas em uma imagem, você precisa usar no mínimo dois pixels para cada área menor que deseja detectar. O tamanho do sensor refere-se a um indicador físico e, via de regra, não é indicado nos dados do passaporte. A melhor maneira de determinar o tamanho de um sensor é observar os parâmetros de pixel nele e multiplicá-lo pela proporção, caso em que o poder de resolução da lente resolve os problemas de uma foto ruim.
Por exemplo, a câmera Basler acA1300-30um tem um tamanho de pixel de 3,75 x 3,75um e uma resolução de 1296 x 966 pixels. O tamanho do sensor é 3,75 µm x 1296 por 3,75 µm x 966=4,86 x 3,62 mm.
O formato do sensor refere-se ao tamanho físico e não depende do tamanho do pixel. Esta configuração é usada paradeterminar com qual lente a câmera é compatível. Para que correspondam, o formato da lente deve ser maior ou igual ao tamanho do sensor. Se for usada uma lente com uma proporção menor, a imagem sofrerá vinhetas. Isso faz com que as áreas do sensor fora da borda do formato da lente fiquem escuras.
Pixels e seleção de câmera

Para ver os objetos na imagem, deve haver espaço suficiente entre eles para que não se fundam com os pixels vizinhos, caso contrário, eles serão indistinguíveis um do outro. Se os objetos são de um pixel cada, a separação entre eles também deve ser de pelo menos um elemento, é graças a isso que se forma um par de linhas, que na verdade tem dois pixels de tamanho. Essa é uma das razões pelas quais é incorreto medir a resolução de câmeras e lentes em megapixels.
Na verdade, é mais fácil descrever as capacidades de resolução de um sistema em termos de frequência de pares de linhas. Segue-se que, à medida que o tamanho do pixel diminui, a resolução aumenta porque você pode colocar objetos menores em elementos digitais menores, ter menos espaço entre eles e ainda resolver a distância entre os assuntos que você fotografa.
Este é um modelo simplificado de como o sensor da câmera detecta objetos sem considerar ruídos ou outros parâmetros, e é a situação ideal.
Gráficos de contraste MTF
A maioria das lentes não são sistemas ópticos perfeitos. A luz que passa através de uma lente sofre um certo grau de degradação. A questão é como avaliar issodegradação? Antes de responder a esta pergunta, é necessário definir o conceito de "modulação". Este último é uma medida da lente de contraste em uma determinada frequência. Pode-se tentar analisar imagens do mundo real tiradas através de uma lente para determinar a modulação ou contraste para detalhes de diferentes tamanhos ou frequências (espaçamento), mas isso é muito impraticável.
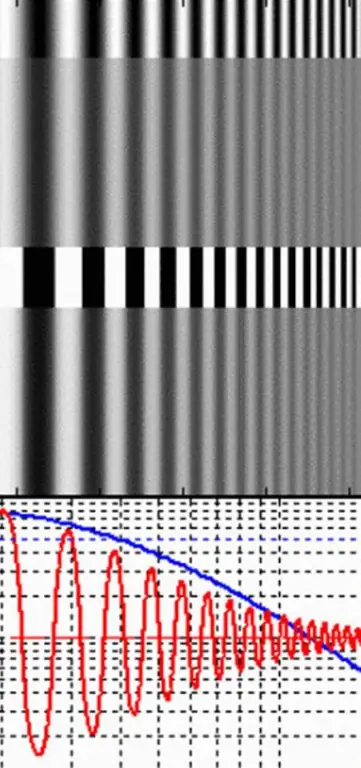
Em vez disso, é muito mais fácil medir a modulação ou contraste para pares de linhas alternadas brancas e escuras. Eles são chamados de rede retangular. O intervalo de linhas em uma grade de onda retangular é a frequência (v), para a qual a função de modulação ou contraste da lente e a resolução são medidas em cm.
A quantidade máxima de luz virá das faixas claras e a mínima das faixas escuras. Se a luz for medida em termos de brilho (L), a modulação pode ser determinada de acordo com a seguinte equação:
modulação=(Lmax - Lmin) / (Lmax + Lmin), onde: Lmax é o brilho máximo das linhas brancas na grade e Lmin é o brilho mínimo das linhas escuras.
Quando a modulação é definida em termos de luz, ela é muitas vezes referida como contraste de Michelson porque leva a relação de luminância das bandas claras e escuras para medir o contraste.
Por exemplo, há uma grade de onda quadrada de uma certa frequência (v) e modulação, e um contraste inerente entre as áreas escuras e claras refletidas dessa grade através da lente. A modulação da imagem e, portanto, o contraste da lente é medido para uma determinada frequênciabarras (v).
A função de transferência de modulação (MTF) é definida como a modulação M i da imagem dividida pela modulação do estímulo (objeto) M o, conforme mostrado na equação a seguir.
|
MTF (v)=M i / M 0 |
USF são impressas em papel a laser 98% brilhante. O toner de impressora a laser preto tem uma refletância de cerca de 10%. Então o valor para M 0 é 88%. Mas como o filme tem uma faixa dinâmica mais limitada em comparação com o olho humano, é seguro assumir que M 0 é essencialmente 100% ou 1. Portanto, a fórmula acima se resume ao seguinte mais equação simples:
|
MTF (v)=Mi |
Então a lente MTF para uma dada frequência de grade (v) é simplesmente a modulação de grade medida (Mi) quando fotografada através de uma lente em um filme.
Resolução do microscópio
A resolução de uma objetiva de microscópio é a distância mais curta entre dois pontos distintos no campo de visão da ocular que ainda podem ser distinguidos como objetos diferentes.
Se dois pontos estiverem mais próximos do que sua resolução, eles parecerão confusos e suas posições serão imprecisas. O microscópio pode oferecer alta ampliação, mas se as lentes forem de baixa qualidade, a baixa resolução resultante degradará a qualidade da imagem.
Abaixo está a equação de Abbe, onde a resoluçãoo poder de uma objetiva de microscópio z é o poder de resolução igual ao comprimento de onda da luz usada dividido por 2 (a abertura numérica da objetiva).
Vários elementos afetam a resolução de um microscópio. Um microscópio óptico ajustado em alta ampliação pode produzir uma imagem desfocada, mas ainda com a resolução máxima da lente.
A abertura digital de uma lente afeta a resolução. O poder de resolução de uma objetiva de microscópio é um número que indica a capacidade de uma lente de coletar luz e resolver um ponto a uma distância fixa da objetiva. O menor ponto que pode ser resolvido pela lente é proporcional ao comprimento de onda da luz coletada dividido pelo número de abertura numérica. Portanto, um número maior corresponde a uma maior capacidade da lente em detectar um excelente ponto no campo de visão. A abertura numérica da lente também depende da quantidade de correção de aberração óptica.
Resolução da lente do telescópio
Como um funil de luz, um telescópio é capaz de coletar luz na proporção da área do furo, esta propriedade é a lente principal.
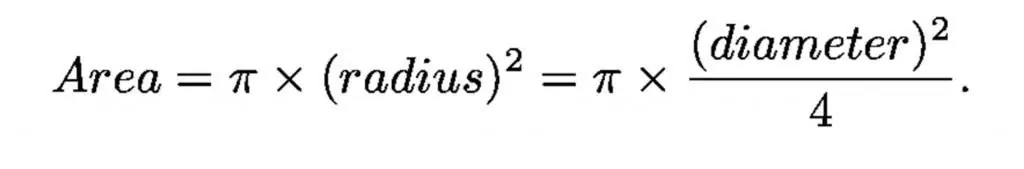
O diâmetro da pupila adaptada ao escuro do olho humano é de pouco menos de 1 centímetro, e o diâmetro do maior telescópio óptico é de 1.000 centímetros (10 metros), de modo que o maior telescópio é um milhão de vezes maior em coleção área do que o olho humano.

É por isso que os telescópios veem objetos mais fracos do que os humanos. E ter dispositivos que acumulam luz usando sensores de detecção eletrônica por muitas horas.
Existem dois tipos principais de telescópio: refratores baseados em lentes e refletores baseados em espelhos. Grandes telescópios são refletores porque os espelhos não precisam ser transparentes. Espelhos de telescópios estão entre os projetos mais precisos. O erro permitido na superfície é de cerca de 1/1000 da largura de um fio de cabelo humano - através de um buraco de 10 metros.
Os espelhos costumavam ser feitos de enormes placas de vidro grosso para evitar que cedessem. Os espelhos de hoje são finos e flexíveis, mas são controlados por computador ou de outra forma segmentados e alinhados por controle de computador. Além da tarefa de encontrar objetos fracos, o objetivo do astrônomo também é ver seus detalhes. O grau em que os detalhes podem ser reconhecidos é chamado de resolução:
- Imagens difusas=baixa resolução.
- Imagens claras=boa resolução.
Devido à natureza ondulatória da luz e fenômenos chamados de difração, o diâmetro do espelho ou lente de um telescópio limita sua resolução final em relação ao diâmetro do telescópio. A resolução aqui significa o menor detalhe angular que pode ser reconhecido. Valores pequenos correspondem a excelentes detalhes da imagem.
Os radiotelescópios devem ser muito grandes para fornecer uma boa resolução. A atmosfera da Terra éimagens turbulentas e desfocadas do telescópio. Os astrônomos terrestres raramente conseguem atingir a resolução máxima do aparelho. O efeito turbulento da atmosfera sobre uma estrela é chamado de visão. Essa turbulência faz com que as estrelas "cintilem". Para evitar esses borrões atmosféricos, os astrônomos lançam telescópios no espaço ou os colocam em altas montanhas com condições atmosféricas estáveis.
Exemplos de cálculo de parâmetros
Dados para determinar a resolução da lente Canon:
- Tamanho do pixel=3,45 µm x 3,45 µm.
- Pixels (A x V)=2448 x 2050.
- Campo de visão desejado (horizontal)=100 mm.
- Limite de resolução do sensor: 1000/2x3, 45=145 lp/mm.
- Dimensões do sensor: 3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Resolução da lente de medição: 145 x 0,0845=12,25 lp/mm.
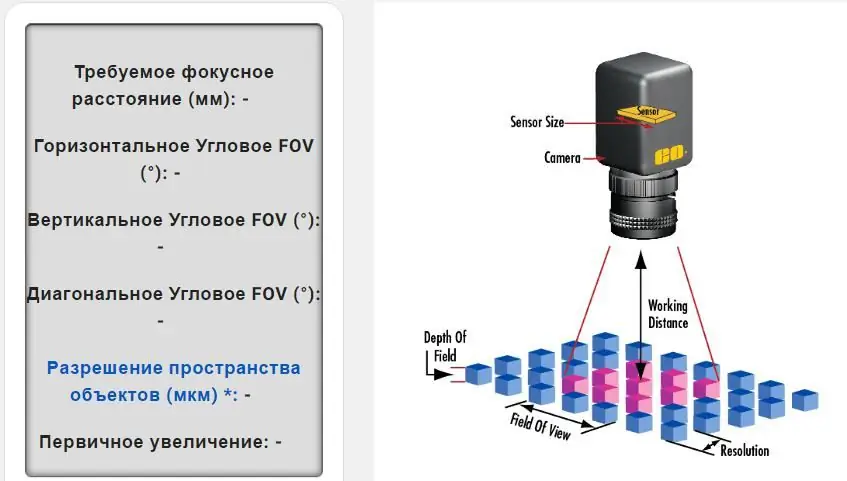
Na verdade, esses cálculos são bastante complexos, mas ajudarão você a criar uma imagem com base no tamanho do sensor, formato de pixel, distância de trabalho e campo de visão em mm. O cálculo desses valores determinará a melhor lente para suas imagens e aplicação.
Problemas da ótica moderna

Infelizmente, dobrar o tamanho do sensor cria problemas adicionais para as lentes. Um dos principais parâmetros que afetam o custo de uma lente de imagem é o formato. Projetar uma lente para um sensor de formato maior requernumerosos componentes ópticos individuais, que deveriam ser maiores e a transferência do sistema mais rígida.
Uma lente projetada para um sensor de 1" pode custar cinco vezes mais do que uma lente projetada para um sensor de ½", mesmo que não possa usar as mesmas especificações com resolução de pixel limitada. O componente de custo deve ser considerado antes de como para determinar o poder de resolução de uma lente.
Imagem óptica hoje enfrenta mais desafios do que uma década atrás. Os sensores com os quais eles são usados têm requisitos de resolução muito mais altos e os tamanhos de formato são simultaneamente reduzidos e maiores, enquanto o tamanho do pixel continua a diminuir.
No passado, a ótica nunca limitava o sistema de imagem, hoje sim. Onde um tamanho de pixel típico é de cerca de 9 µm, um tamanho muito mais comum é de cerca de 3 µm. Esse aumento de 81x na densidade de pontos afetou a ótica e, embora a maioria dos dispositivos seja boa, a seleção de lentes agora é mais importante do que nunca.






