Na avaliação por pares, por exemplo, para avaliar a competitividade de produtos, é necessário, como em qualquer trabalho científico, realizar o tratamento estatístico dos dados. Este último começa com a determinação da consistência das opiniões dos especialistas, cuja expressão numérica é o coeficiente de concordância.
Por que precisamos de uma avaliação por consenso de especialistas?
Esta avaliação é necessária, em primeiro lugar, porque as opiniões dos especialistas podem diferir muito sobre os parâmetros estimados. Inicialmente, a avaliação é realizada classificando os indicadores e atribuindo-lhes um determinado coeficiente de significância (peso). Uma classificação inconsistente faz com que esses coeficientes sejam estatisticamente não confiáveis. As opiniões de especialistas com seu número exigido (mais de 7-10) devem ser distribuídas de acordo com a lei normal.
O conceito do coeficiente de concordância
Então. Consistência é concordância. O coeficiente é uma quantidade adimensional que mostra a razão entre a dispersão e a dispersão máxima no caso geral. Vamos generalizar esses conceitos.
Coeficiente de concordância é um número de 0 a 1, mostrando a consistência das opiniões de especialistas quandoclassificação de algumas propriedades. Quanto mais próximo este valor estiver de 0, menor será a consistência considerada. Se o valor desse coeficiente for inferior a 0,3, as opiniões dos especialistas são consideradas inconsistentes. Quando o valor do coeficiente está na faixa de 0,3 a 0,7, a consistência é considerada média. Um valor maior que 0,7 é considerado alta consistência.
Casos de uso
Ao realizar uma pesquisa estatística, podem surgir situações em que um objeto pode ser caracterizado não por duas sequências, que são estatisticamente processadas pelo coeficiente de concordância, mas por várias sequências, que são classificadas de acordo com especialistas com o mesmo nível de profissionalismo em determinada área.
A consistência da classificação realizada pelos especialistas deve ser determinada para confirmar a exatidão da hipótese de que os especialistas fazem medições relativamente precisas, o que permite a formação de vários agrupamentos em grupos de especialistas, que são em grande parte determinados por fatores humanos, principalmente como diferenças de pontos de vista, conceitos, diferentes escolas científicas, a natureza da atividade profissional, etc.
Breve descrição do método de classificação. Suas vantagens e desvantagens
Na classificação, o método de classificação é usado. Sua essência reside no fato de que cada propriedade do objeto recebe sua própria classificação específica. Além disso, a cada especialista incluído no grupo de especialistas, essa classificação é atribuídade forma independente, resultando na necessidade de processar esses dados para identificar a consistência das opiniões dos especialistas. Este processo é realizado calculando o coeficiente de concordância.
A principal vantagem do método rank é sua facilidade de implementação.
As principais desvantagens do método são:
- um pequeno número de objetos de classificação, pois quando seu número excede 15-20, torna-se difícil atribuir pontuações de classificação objetivas;
- Com base no uso deste método, a questão de quão longe os objetos estudados estão um do outro em significado permanece em aberto.
Ao utilizar este método, deve-se levar em consideração que as classificações são baseadas em algum tipo de modelo probabilístico, portanto, devem ser aplicadas com cautela, dada a abrangência.
Coeficiente de classificação de concordância de Kendall
Usado para determinar a relação entre as características quantitativas e qualitativas que caracterizam objetos homogêneos e classificados de acordo com o mesmo princípio.
Este coeficiente é determinado pela fórmula:
t=2S/(n(n-1)), onde
S - a soma das diferenças entre o número de sequências e o número de inversões no segundo recurso;
n - número de observações.

Algoritmo de cálculo:
- Os valores x são classificados em ordem crescente ou decrescente.
- Os valores de y são organizados na ordem em que correspondem aos valores de x.
- Para cada rank sucessivo de y, determine quantos valores de rank mais altos o seguem. Eles são somados e a medida de correspondência das sequências de ranks em xey é calculada.
- Da mesma forma, é calculado o número de fileiras de y com valores mais baixos, que também somam.
- Adicione o número de ranks com valores mais altos e o número de ranks com valores mais baixos, resultando no valor S.
Este coeficiente mostra a relação entre duas variáveis e, na maioria dos casos, é chamado de coeficiente de correlação de Kendall. Tal dependência pode ser representada graficamente.
Determinação do coeficiente
Como é feito? Se o número de características ou fatores classificados exceder 2, o coeficiente de concordância é usado, que, em essência, é uma variante múltipla da correlação de classificação.
Tenha cuidado. O cálculo do coeficiente de concordância é baseado na razão do desvio da soma dos quadrados dos postos da soma média dos quadrados dos postos, multiplicada por 12, para o quadrado dos especialistas, multiplicado pela diferença entre o cubo do número de objetos e o número de objetos.
Algoritmo de cálculo
Para entender de onde vem o número 12 no numerador da fórmula de cálculo, vejamos o algoritmo de determinação.
Para cada linha com os ranks de um determinado expert, é calculada a soma dos ranks, que é um valor aleatório.
O coeficiente de concordância é geralmente definido como a razão da estimativa de variância (D) para o valor máximo da estimativa de variância(Dmax). Vamos formular sucessivamente as definições dessas quantidades.
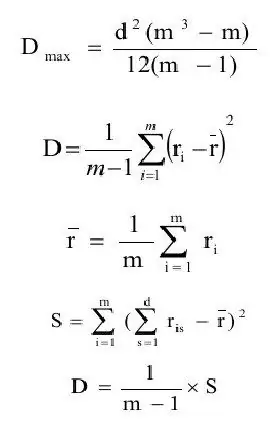
onde ravg - estimativa de expectativa;
m - número de objetos.
Substituindo as fórmulas resultantes em relação a D para Dmax obtemos a fórmula final para o coeficiente de concordância:
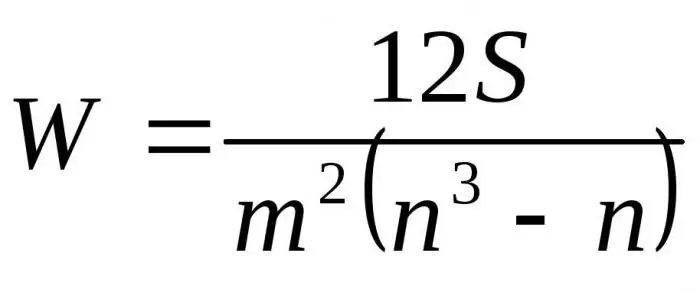
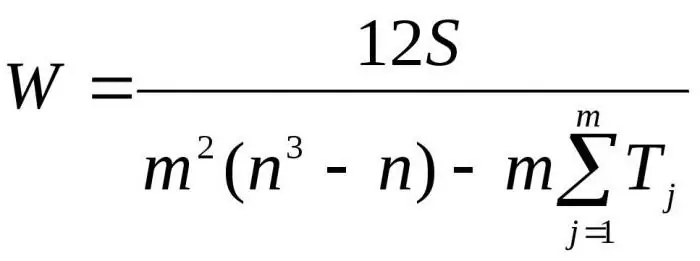
Aqui m é o número de especialistas, n é o número de objetos.
A primeira fórmula é usada para determinar o fator de concordância se não houver ranks relacionados. A segunda fórmula é usada se houver classificações relacionadas.
Então, o cálculo do coeficiente de concordância está encerrado. Qual é o próximo? O valor obtido é avaliado quanto à significância utilizando o coeficiente de Pearson, multiplicando este coeficiente pelo número de especialistas e pelo número de graus de liberdade (m-1). O critério resultante é comparado com o valor da tabela, e se o valor do primeiro exceder o último, eles falam da significância do coeficiente em estudo.
No caso de ranks relacionados, o cálculo do critério de Pearson torna-se um pouco mais complicado e é realizado pela seguinte razão: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Exemplo
Assuma que o método especialista avalia a competitividade da manteiga vendida em uma rede varejista. Vamos dar um exemplo de cálculo do coeficiente de concordância. Antes de avaliar a competitividade, é necessário classificar o consumidorpropriedades deste produto que estão envolvidas na avaliação. Vamos supor que essas propriedades sejam as seguintes: sabor e cheiro, consistência e aparência, cor, embalagem e rotulagem, teor de gordura, nome comercial, fabricante, preço.
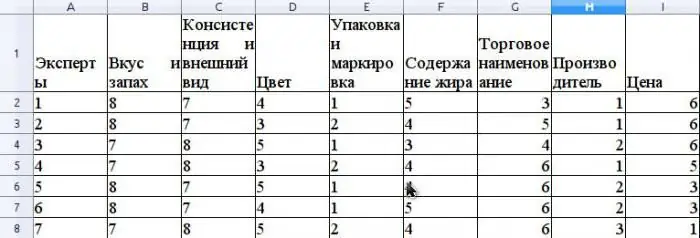
Assuma que o grupo de especialistas é composto por 7 especialistas. A figura mostra os resultados da classificação dessas propriedades.
O valor médio de r é calculado como a média aritmética e será 31,5. Para encontrar S, some as diferenças quadradas entre ris e r média, de acordo com a fórmula acima e determine que o valor de S é 1718.
Calcule o coeficiente de concordância usando a fórmula sem usar classificações relacionadas (as classificações seriam relacionadas se o mesmo Expert Advisor tivesse as mesmas classificações para propriedades diferentes).
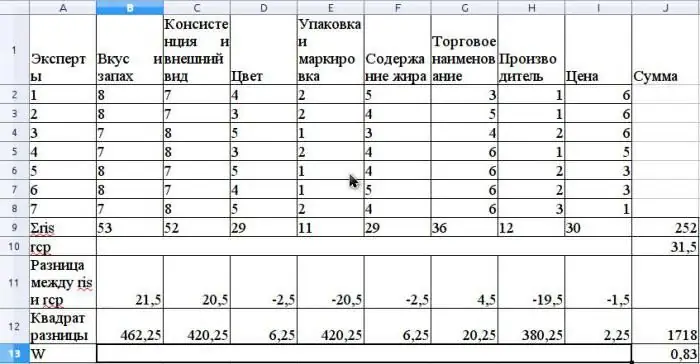
O valor desse coeficiente será 0,83. Isso indica um forte consenso entre os especialistas.
Verifique sua significância usando o teste de Pearson:
7 x 0,83 x (8-1)=40,7.
Teste tabular de Pearson em nível de significância de 1% é 18,5 e em 5% - 14,1..
O exemplo demonstra a simplicidade e acessibilidade do cálculo para qualquer pessoa que conheça o básico de cálculos matemáticos. Para aliviá-los,use formulários de planilha.
Em conclusão
Assim, o coeficiente de concordância mostra a consistência das opiniões de vários especialistas. Quanto mais distante de 0 e mais próximo de 1, mais consistentes são as opiniões. Esses coeficientes devem ser confirmados pelo cálculo do critério de Pearson.






