A regra de Titius-Bode (às vezes simplesmente chamada de lei de Bode) é a hipótese de que os corpos em alguns sistemas orbitais, incluindo o Sol, giram ao longo de semi-eixos dependendo da sequência planetária. A fórmula sugere que, estendendo-se para fora, cada planeta estará cerca de duas vezes mais distante do Sol que o anterior.
A hipótese previu corretamente as órbitas de Ceres (no cinturão de asteróides) e Urano, mas falhou em determinar a órbita de Netuno e acabou sendo substituída pela teoria da formação do sistema solar. É nomeado após Johann Daniel Titius e Johann Elert Bode.

Origens
A primeira menção de uma série que se aproxima da lei de Bode pode ser encontrada em Elements of Astronomy, de David Gregory, publicado em 1715. Nele ele diz: “… supondo que a distância do Sol à Terra seja dividida em dez partes iguais, das quais a distância de Mercúrio será de cerca de quatro, de Vênus sete, de Marte quinze, de Júpiter cinquenta e duas, e de Saturno noventa e cinco . Uma sugestão semelhante, provavelmente inspirada por Gregory, aparece em um trabalho publicado por Christian Wolff em 1724.
Em 1764, Charles Bonnet, em seu livro Contemplation of Nature, disse: "Conhecemos os dezessete planetas que compõem nosso sistema solar [isto é, os principais planetas e seus satélites], mas não temos certeza de que eles não são mais." A isso, em sua tradução de 1766 da obra de Bonnet, Johann Daniel Titius acrescentou dois parágrafos de sua autoria no final da página 7 e no topo da página 8. O novo parágrafo interpolado não é encontrado no texto original de Bonnet: nem no italiano nem traduções em inglês da obra.
Descoberta de Titius
Há duas partes no texto intercalado de Tício. A primeira explica a sequência de distâncias planetárias do Sol. Ele também contém algumas palavras sobre a distância do Sol a Júpiter. Mas este não é o fim do texto.
Vale a pena dizer algumas palavras sobre a fórmula da regra de Titius-Bode. Preste atenção às distâncias entre os planetas e descubra que quase todos eles estão separados uns dos outros na proporção correspondente ao tamanho de seus corpos. Divida a distância do Sol a Saturno por 100 partes; então Mercúrio é separado por quatro dessas partes do Sol; Vênus - em 4 + 3=7 dessas partes; Terra - por 4+6=10; Marte - por 4+12=16.
Mas note que de Marte a Júpiter há um desvio dessa progressão tão precisa. Um espaço de 4+24=28 dessas partes segue de Marte, mas até agora nenhum planeta foi descoberto lá. Mas o Lorde Arquiteto deveria deixar este lugar vazio? Nunca. entãovamos supor que este espaço pertença sem dúvida às luas de Marte ainda não descobertas, e acrescentar que talvez Júpiter ainda tenha algumas luas menores ao seu redor que ainda não foram vistas por nenhum telescópio.

Ascensão do Bode
Em 1772, Johann Elert Bode, com a idade de vinte e cinco anos, completou a segunda edição de seu compêndio astronômico Anleitung zur Kenntniss des gestirnten Himmels ("Guia para o conhecimento do céu estrelado"), ao qual ele adicionou a seguinte nota de rodapé, originalmente sem fonte, mas anotada em versões posteriores. Nas memórias de Bode pode-se encontrar uma referência a Tício com um claro reconhecimento de sua autoridade.

Opinião Bode
É assim que a regra de Titius-Bode na apresentação deste último soa: se a distância do Sol a Saturno for igual a 100, então Mercúrio é separado do Sol por quatro dessas partes. Vênus - 4+3=7. Terra - 4+6=10. Marte - 4+12=16.
Agora há uma lacuna nessa progressão ordenada. Depois de Marte segue-se um espaço com um cálculo de 4+24=28, no qual ainda não foi visto um único planeta. Podemos acreditar que o Fundador do universo deixou este espaço vazio? Claro que não. A partir daqui chegamos à distância de Júpiter na forma de cálculo 4+48=52 e, finalmente, à distância de Saturno - 4+96=100.

Estas duas afirmações sobre todas as tipologias específicas e raios orbitais parecem vir deastronomia. Muitas dessas teorias datam de antes do século XVII.
Influência
Titius foi aluno do filósofo alemão Christian Freiherr von Wolff (1679-1754). A segunda parte do texto inserido na obra de Bonnet é baseada na obra de von Wolff de 1723, Vernünftige Gedanken von den Wirkungen der Natur.
A literatura do século XX atribui a autoria da regra de Titius-Bode a um filósofo alemão. Nesse caso, Titius poderia aprender com ele. Outra referência mais antiga foi escrita por James Gregory em 1702 em seu Astronomiae Physicae et geometryae Elementa, onde a sequência de distâncias planetárias 4, 7, 10, 16, 52 e 100 tornou-se uma progressão geométrica da razão 2.
Esta é a fórmula mais próxima de Newton, e também foi encontrada nos escritos de Benjamin Martin e Thomas Ceard anos antes do livro de Bonnet ser publicado na Alemanha.
Trabalho adicional e implicações práticas
Titius e Bode esperavam que a lei levasse à descoberta de novos planetas e, de fato, a descoberta de Urano e Ceres, cuja distância entre eles concorda bem com a lei, contribuiu para sua aceitação pelo mundo científico.
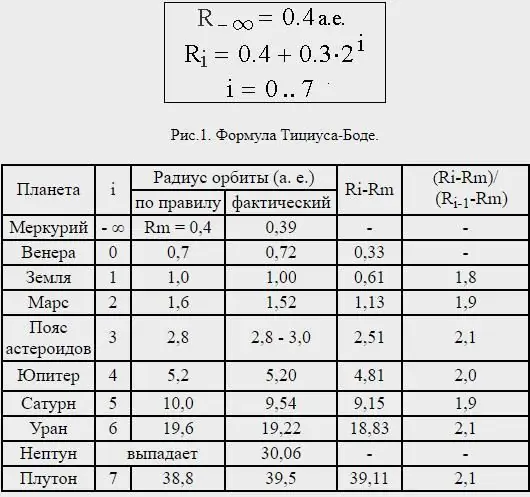
No entanto, a distância de Netuno era muito inconsistente e, de fato, Plutão - agora não considerado um planeta - está a uma distância média que corresponde aproximadamente à lei de Titius-Bode prevista para o próximo planeta fora de Urano.
A lei originalmente publicada foi aproximadamente satisfeita por todos os planetas conhecidos - Mercúrio e Saturno - com uma lacuna entrequarto e quinto planetas. Esta foi considerada uma figura interessante, mas não de grande importância, até a descoberta de Urano em 1781, que se encaixa na série.
Com base nessa descoberta, Bode pediu uma busca por um quinto planeta. Ceres, o maior objeto do cinturão de asteroides, foi encontrado na posição prevista de Bode em 1801. A lei de Bode foi amplamente aceita até que Netuno foi descoberto em 1846 e mostrou ser inconsistente com a lei.
Ao mesmo tempo, um grande número de asteroides descobertos no cinturão cruzaram Ceres fora da lista de planetas. A lei de Bode foi discutida pelo astrônomo e lógico Charles Sanders Peirce em 1898 como um exemplo de raciocínio falacioso.

Desenvolvimento do problema
A descoberta de Plutão em 1930 complicou ainda mais o problema. Embora não correspondesse à posição prevista pela lei de Bode, tratava-se da posição que a lei previa para Netuno. No entanto, a descoberta subsequente do cinturão de Kuiper, e em particular do objeto Eris, que é mais massivo que Plutão, mas não está de acordo com a lei de Bode, desacreditou ainda mais a fórmula.
Contribuição de Serda
O jesuíta Thomas Cerda deu o famoso curso de astronomia em Barcelona em 1760 na Cátedra Real de Matemática do Colégio de Sant Jaume de Cordelle (Seminário Imperial e Real dos Nobres de Cordell). No Tratado de Cerdas aparecem as distâncias planetárias, obtidas pela aplicação da terceira lei de Kepler, com precisão de 10-3.
Se tomarmos como 10 a distância da Terra earredondar para inteiro, progressão geométrica [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, de n=2 a n=8, pode ser expressa. E usando um movimento fictício circular uniforme para a anomalia de Kepler, os valores de Rn correspondentes às razões de cada planeta podem ser obtidos como rn=(Rn - R1) / (Rn-1 - R1), resultando em 1,82; 1, 84; 1, 86; 1,88 e 1,90, onde rn=2 - 0,02 (12 - n) é uma relação explícita entre a continuidade Kepleriana e a lei de Titius-Bode, que é considerada uma coincidência numérica aleatória. O resultado do cálculo é próximo de dois, mas o deuce pode ser considerado como um arredondamento do número 1, 82.

A velocidade média do planeta de n=1 a n=8 reduz a distância do Sol e difere do declínio uniforme em n=2 para recuperar de n=7 (ressonância orbital). Isso afeta a distância do Sol a Júpiter. No entanto, a distância entre todos os outros objetos dentro do quadro da notória regra a que o artigo se dedica também é determinada por essa dinâmica matemática.
Aspecto teórico
Não há uma explicação teórica sólida subjacente à regra de Titius-Bode, mas é possível que, dada a combinação de ressonância orbital e f alta de graus de liberdade, qualquer sistema planetário estável tenha uma alta probabilidade de repetir o modelo descrito em esta teoria pelos dois cientistas.
Como isso pode ser uma coincidência matemática e não uma "lei da natureza", às vezes é chamado de regra em vez de "lei". No entanto, o astrofísico Alan Boss argumenta que isso é simplesmentecoincidência, e a revista científica planetária Icarus não está mais aceitando artigos que tentem fornecer versões melhoradas da "lei".
Ressonância orbital
Ressonância orbital de grandes corpos em órbita cria regiões ao redor do Sol que não têm órbitas estáveis de longo prazo. Os resultados da simulação de formação de planetas apoiam a ideia de que um sistema planetário estável escolhido aleatoriamente provavelmente satisfará a regra de Titius-Bode.

Dubrulle e Graner
Dubrulle e Graner mostraram que as regras de distância da lei de potência podem ser consequência de modelos de nuvens em colapso de sistemas planetários que possuem duas simetrias: invariância rotacional (a nuvem e seu conteúdo são axissimétricos) e invariância de escala (a nuvem e seu conteúdo parece o mesmo em todas as escalas).
Esta última é uma característica de muitos fenômenos que se acredita desempenharem um papel na formação de planetas, como a turbulência. A distância do Sol aos planetas do sistema solar, proposta por Titius e Bode, não foi revisada no âmbito dos estudos de Dubrulle e Graner.






