Ao estudar física na 10ª série, o tópico dos dipolos é considerado. O que significa esse conceito e quais fórmulas são usadas para calculá-lo?
Introdução
Se você colocar um dipolo no espaço de um campo elétrico uniforme, você pode representá-lo como linhas de força. Um dipolo é um sistema no qual existem duas cargas que são idênticas em parâmetros, mas são cargas puntiformes opostas. Além disso, a distância entre eles será muito menor do que a distância a qualquer ponto do campo dipolar. O conceito de momento dipolar é estudado no curso escolar de eletrodinâmica (10º ano).
O eixo do dipolo é uma linha reta que passa pelos pontos de ambas as cargas. Um braço dipolo é um vetor que conecta uma carga e, ao mesmo tempo, passa de partículas carregadas negativamente para partículas carregadas positivamente. Um dipolo elétrico é caracterizado pela presença de um estado como um dipolo ou momento elétrico.
Por definição, um momento de dipolo é um vetor que é numericamente igual ao produto da carga do dipolo e seu braço. Além disso, é co-dirigido com o ombro do dipolo. Na igualdade zero da soma das forças, calculamos o valor do momento. Para o ângulo que existe entre o momento de dipolo edirecionalidade do campo elétrico, a presença de um momento mecânico é característica.
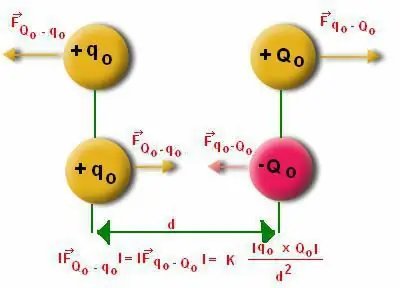
Muitas vezes as pessoas acham difícil calcular o módulo que atua na estrutura do dipolo. Aqui é necessário levar em conta as peculiaridades do cálculo do ângulo "Alpha". Sabe-se que o dipolo se desvia da posição de equilíbrio. Mas o próprio momento de dipolo tem um caráter restaurador, pois tende a estar em movimento.
Cálculos
Quando este momento de dipolo é colocado no meio de um campo elétrico não homogêneo, surge inevitavelmente uma força. Em tal ambiente, os indicadores da soma de forças não serão zero. Consequentemente, existem forças atuando no momento de dipolo com caráter pontual. O tamanho do braço dipolo é muito menor.
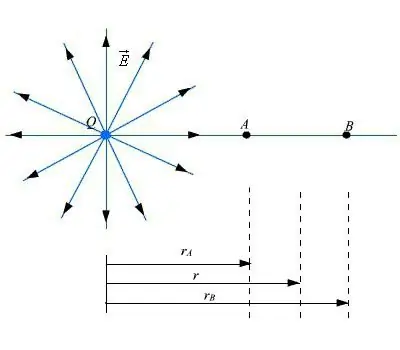
A fórmula pode ser escrita assim: F=q (E2 - E1)=qdE, onde d é o diferencial do campo elétrico.
Pesquisar as características do conceito físico em estudo
Vamos examinar o assunto mais a fundo. Para determinar qual é a característica do campo elétrico, se ele é criado usando um sistema de cargas e localizado em um pequeno espaço, é necessário fazer vários cálculos. Um exemplo é apresentado pelos átomos e moléculas, que em sua composição possuem núcleos e elétrons eletricamente carregados.
Se for necessário buscar um campo a uma distância maior que as dimensões que compõem a área onde as partículas estão localizadas, usaremos algumas fórmulas exatas de alta complexidade. É possível usar mais simplesexpressões aproximadas. Suponhamos que conjuntos pontuais de cargas qk participem da criação do campo elétrico. Eles estão localizados em um espaço pequeno.
Para realizar o cálculo da característica que o campo possui, é permitido combinar todas as cargas do sistema. Tal sistema é considerado como uma carga pontual Q. Os indicadores de magnitude serão a soma das cargas que estavam no sistema original.
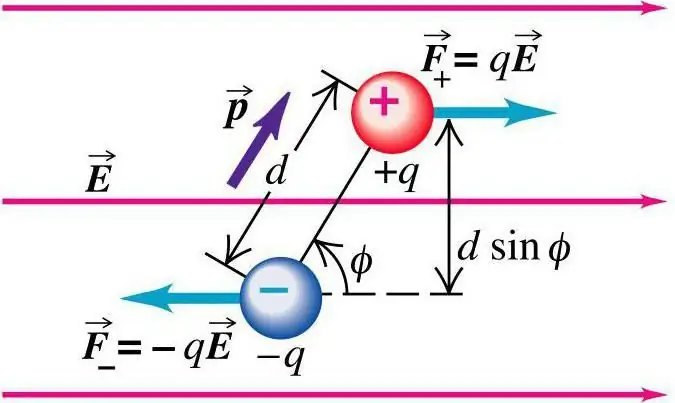
Localização das cobranças
Vamos imaginar que a localização da carga seja indicada em qualquer lugar onde o sistema de cargas qk esteja localizado. Ao fazer alterações no local, caso este tenha limites expressos em uma pequena área, tal influência será desprezível, quase imperceptível ao campo do ponto de vista. Dentro desses limites de aproximação de força e potencial que o campo elétrico possui, as determinações são feitas usando fórmulas tradicionais.
Quando a soma da carga total do sistema for zero, os parâmetros da aproximação indicada parecerão grosseiros. Isso dá razão para concluir que o campo elétrico está simplesmente ausente. Se for necessário obter uma aproximação mais precisa, colete mentalmente grupos separados de cargas positivas e negativas do sistema que está sendo considerado.
No caso de deslocamento de seus "centros" em relação a outros, os parâmetros de campo em tal sistema podem ser descritos como um campo que possui duas cargas puntiformes, iguais em magnitude e de sinais opostos. Nota-se que eles estão deslocados em relação aos demais. FornecerPara uma caracterização mais precisa do sistema de cargas em termos dos parâmetros desta aproximação, será necessário estudar as propriedades de um dipolo em um campo elétrico.
Introdução do termo
Voltemos à definição. Um dipolo elétrico é a definição de um sistema que tem duas cargas puntiformes. Eles têm o mesmo tamanho e sinais opostos. Além disso, tais sinais estão localizados a pequenas distâncias em relação a outros sinais.
Você pode calcular a característica do processo que é criado por meio de um dipolo, e é representado por duas cargas puntiformes: +q e −q, e estão localizadas a uma distância a em relação às demais.

Sequência de cálculos
Vamos começar calculando o potencial e a intensidade que o dipolo tem em sua superfície axial. Esta é uma linha reta que corre entre duas cargas. Desde que o ponto A esteja localizado a uma distância igual a r em relação à parte central do dipolo, e se for r >> a, de acordo com o princípio da superposição para o potencial de campo neste ponto, será racional use a expressão para calcular os parâmetros do dipolo elétrico.
A magnitude do vetor de força é calculada pelo princípio da superposição. Para calcular a força de campo, é usado o conceito de razão entre potencial e força de campo:
Ex=−Δφ /Δx.
Nessas condições, a direção do vetor de intensidade é indicada longitudinalmente em relação ao eixo do dipolo. Para calcular seu módulo, a fórmula padrão é aplicável.
Importanteesclarecimentos
Deve-se levar em conta que o enfraquecimento do campo de dipolo elétrico ocorre mais rápido do que ele experimenta uma carga pontual. O decaimento do potencial de campo dipolar é inversamente proporcional ao quadrado da distância, e a intensidade do campo é inversamente proporcional ao cubo da distância.
Usando métodos semelhantes, mas mais complicados, os parâmetros do potencial e da intensidade de campo do dipolo são encontrados em pontos arbitrários, cujos parâmetros de posição são determinados usando um método de cálculo como coordenadas polares: a distância até o centro do dipolo elétrico (r) e o ângulo (θ).
Cálculo usando vetor de tensão
O conceito do vetor intensidade E é dividido em dois pontos:
- Radial (Er), que é direcionado no sentido longitudinal em relação à linha reta.
- Tal linha reta conecta o ponto especificado e o centro do dipolo com a perpendicular a ele Eθ.
Esta decomposição de cada componente é direcionada ao longo do curso da mudança que ocorre com todas as coordenadas do ponto a ser observado. Você pode encontrá-lo pela razão que relaciona os indicadores de intensidade de campo a possíveis modificações.
Encontrando a componente vetorial na intensidade do campo, é importante estabelecer a natureza da relação nas mudanças de potencial que ocorrem devido ao deslocamento do ponto de observação na direção dos vetores.
Calcule a componente perpendicular
Quando terminarPara este procedimento, é importante levar em consideração que a expressão para a magnitude em um pequeno deslocamento perpendicular será determinada alterando o ângulo: Δl=rΔθ. Os parâmetros de magnitude para esta componente de campo serão iguais.
Tendo obtido a razão, é possível determinar o campo do dipolo elétrico em um ponto arbitrário para construir uma imagem com as linhas de força desse campo.
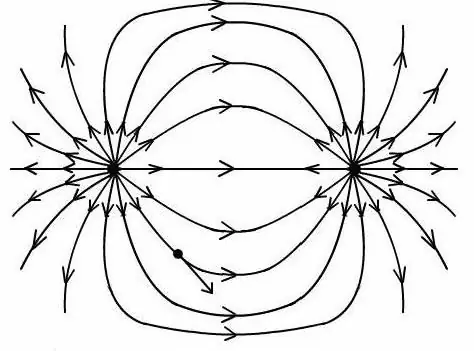
É importante considerar que todas as fórmulas para determinar o potencial e a intensidade de campo de um dipolo operam apenas no produto dos valores que uma carga de dipolo possui e a distância entre eles.
Momento dipolar
O título do trabalho descrito é uma descrição completa do tipo elétrico de propriedades. Tem o nome de "momento dipolar do sistema".
Por definição de dipolo, que é um sistema de cargas puntiformes, pode-se verificar que ele se caracteriza pela presença de simetria axial, quando o eixo é uma linha reta que passa por várias cargas.
Para definir a característica completa do dipolo, indique a direção de orientação que o eixo possui. Para simplificar os cálculos, o vetor momento dipolar pode ser especificado. O valor de sua magnitude é igual à magnitude do momento de dipolo, e o vetor de direção difere pela coincidência dele e do eixo do dipolo. Então, p=qa se a é a direção do vetor que conecta as cargas negativas e positivas do dipolo.
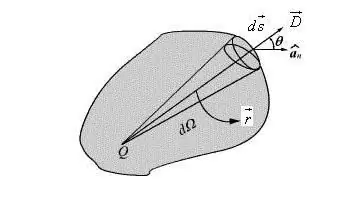
O uso de tal característica do dipolo é conveniente e torna possível na maioria dos casos simplificar a fórmula e dar-lhe a formavetor. A descrição do potencial do campo dipolar em um ponto de direção arbitrária é escrita na forma de um vetor.
A introdução de conceitos como a característica vetorial de um dipolo e seu momento de dipolo pode ser realizada usando um modelo simplificado − uma carga pontual em um campo uniforme, que inclui um sistema de cargas, cujas dimensões geométricas não não precisa ser levado em consideração, mas é importante conhecer o momento dipolar. Este é um pré-requisito para realizar cálculos.
Como se comporta um dipolo
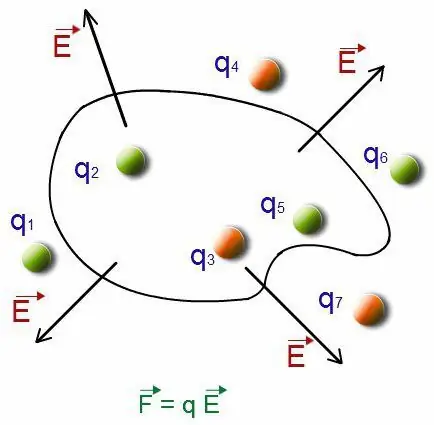
O comportamento de um dipolo pode ser visto no exemplo de tal situação. A posição de duas cargas puntiformes tem um caráter fixo de distância uma em relação à outra. Eles foram colocados nas condições de um dipolo de um campo elétrico uniforme. Fez observações sobre o processo. Nas aulas de física (eletrodinâmica), esse conceito é considerado em detalhes. Do campo para a carga, realiza-se a ação das forças:
F=±qE
Eles são iguais em magnitude e opostos em direção. O indicador da força total que atua no dipolo é zero. Como tal força tem efeito em vários pontos, o momento total será:
M=Fa sen a=qEa sen a=pE sen a
com α sendo o ângulo que conecta os vetores de intensidade de campo e os vetores de momento de dipolo. Devido à presença de um momento de força, o momento de dipolo do sistema tende a retornar às direções do vetor de intensidade do campo elétrico.
Dipolo elétrico é um conceito que é importante entender claramente. Você pode ler mais sobre isso na Internet. Também podepara estudar nas aulas de física na escola na 10ª série, como falamos acima.






