Quanto mais velhos os alunos ficam, mais há necessidade de rapidez na resolução de problemas simples. Não é dado muito tempo em exames para resolver exemplos ou problemas simples por muito tempo. Como encontrar a diagonal de um quadrado de forma rápida e fácil? Isso é ensinado para crianças a partir da oitava série. Este artigo mostra duas maneiras - uma é mais longa, a outra é mais rápida.
Como calcular a diagonal de um quadrado?
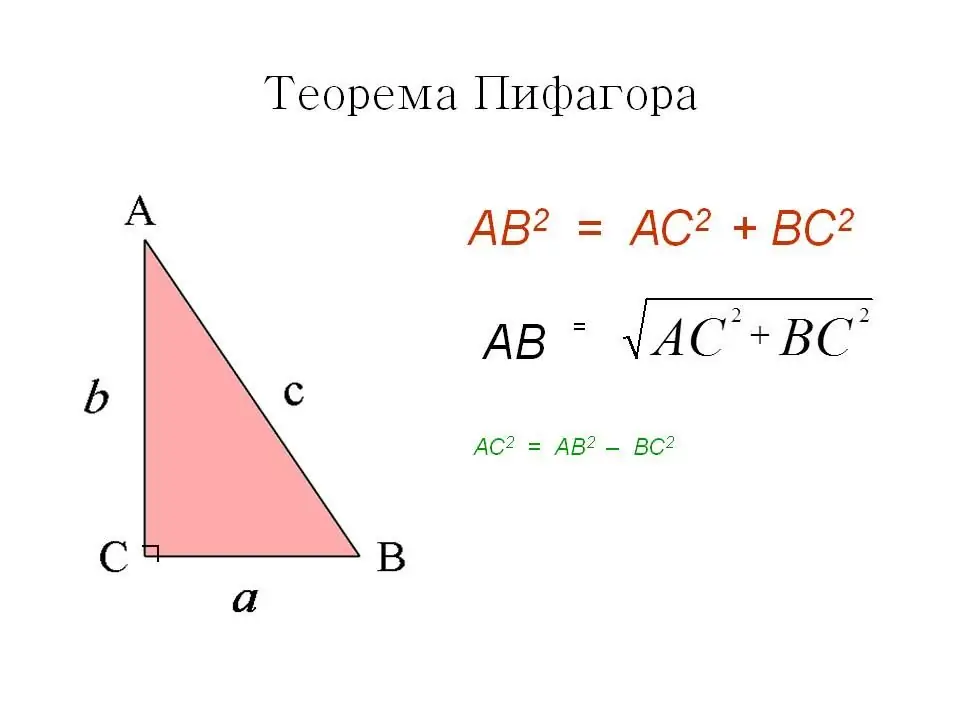
A primeira maneira é o bem conhecido e familiar teorema de Pitágoras. Em um quadrado, todos os ângulos são retos, o que significa que a diagonal o divide em dois triângulos retângulos iguais e é em si sua hipotenusa. De acordo com o teorema de Pitágoras, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

A segunda maneira é uma fórmula simples que é exclusiva dos quadrados, e você só precisa se lembrar dela. Como você sabe, todos os lados de um quadrado são iguais, e é por isso que os matemáticos calcularam a seguinte fórmula para encontrar sua diagonal: é igual ao produto do lado pela raiz de dois.
Claro, é melhor apenas lembrar a fórmula para o comprimento da diagonal de um quadrado e usá-la sempre, porque é muito mais rápido e conveniente. Isso é especialmente sentido ao resolver problemas na forma literal, onde em vez de expressões de raiz inteiras grandes, você pode se virar com apenas um produto.
Exemplo
Tome, por exemplo, um quadrado de 6 por 6, ou seja, com lado igual a seis centímetros.
De acordo com o primeiro método: seja a diagonal C e o lado A.
Então temos que C=√A^2+A^2 ou C=√2A^2.
Vamos escrever na forma numérica: С=√36 + 36. Temos √72, que é 3√8 ou 6√2.
E agora vamos encontrar a mesma diagonal, mas pelo segundo método: C=A√2 ou na forma numérica: 6√2
Agora você pode ver o quanto o segundo método é mais rápido, fácil e o mais importante - mais eficiente, especialmente em problemas tão fáceis, porque cada minuto é precioso no exame!
Outras propriedades das diagonais quadradas
Além de saber como encontrar as diagonais de um quadrado, você também precisa conhecer suas propriedades. Os principais são:
- As diagonais são iguais entre si e o ponto de interseção é dividido ao meio.
- Eles formam ângulos retos quando se cruzam.
- Divida o quadrado em triângulos iguais.
Conclusão
A questão de como contar as diagonais de um quadrado geralmente é feita por alunos que perderam este tópico na escola. No entanto, todos deveriam conhecer essas regras fundamentais da matemática! É desejável resolver o mais rápido possível, e isso requer o conhecimento de fórmulas abreviadas. Tudo isso é extremamente simples e fácil, masao mesmo tempo, é a base necessária para resolver problemas muito mais complexos no futuro. E uma parte importante desta base é o quadrado.






