Estudar os processos que ocorrem em sistemas estatísticos é complicado pelo tamanho mínimo das partículas e seu grande número. É praticamente impossível considerar cada partícula separadamente, portanto, são introduzidas quantidades estatísticas: a velocidade média das partículas, sua concentração, massa das partículas. A fórmula que caracteriza o estado do sistema, levando em consideração parâmetros microscópicos, é chamada de equação básica da teoria cinética molecular dos gases (MKT).
Um pouco sobre a velocidade média das partículas
A determinação da velocidade das partículas foi realizada pela primeira vez experimentalmente. Um conhecido experimento do currículo escolar, conduzido por Otto Stern, possibilitou criar uma ideia de velocidades de partículas. Durante o experimento, estudou-se o movimento dos átomos de prata em cilindros rotativos: primeiro, no estado estacionário da instalação, depois quando ela girava com certa velocidade angular.
Como resultado, verificou-se que a velocidade das moléculas de prata excede a velocidade do som e é de 500 m/s. O fato é bastante interessante, pois é difícil para uma pessoa sentir tais velocidades de movimento de partículas em substâncias.
Gás Ideal
Continuar pesquisandoParece possível apenas em um sistema cujos parâmetros podem ser determinados por medições diretas usando instrumentos físicos. A velocidade é medida com um velocímetro, mas a ideia de prender um velocímetro a uma única partícula é absurda. Apenas um parâmetro macroscópico associado ao movimento de partículas pode ser medido diretamente.
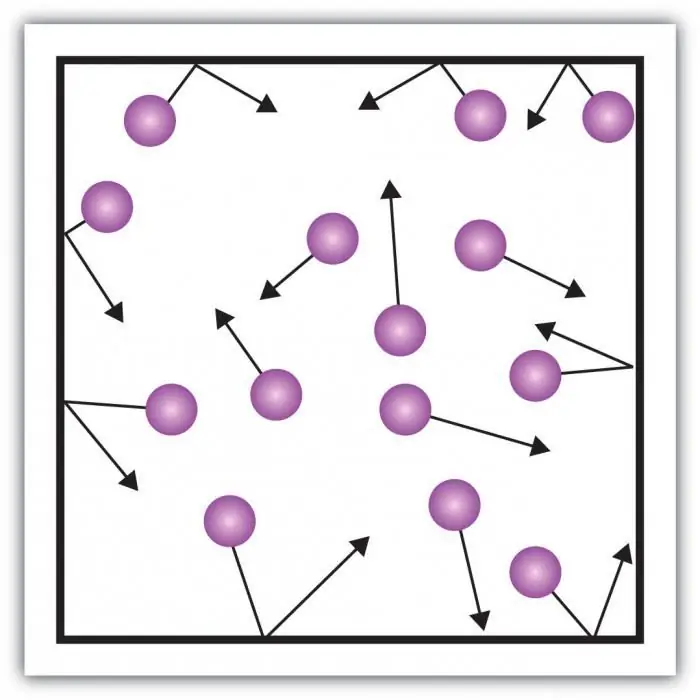
Considere a pressão do gás. A pressão nas paredes do vaso é criada pelos impactos das moléculas do gás no vaso. A peculiaridade do estado gasoso da matéria está em distâncias suficientemente grandes entre as partículas e sua pequena interação entre si. Isso permite que você meça diretamente sua pressão.
Qualquer sistema de corpos em interação é caracterizado pela energia potencial e energia cinética do movimento. O gás real é um sistema complexo. A variabilidade da energia potencial não se presta à sistematização. O problema pode ser resolvido introduzindo um modelo que carregue as propriedades características do gás, deixando de lado a complexidade da interação.
Gás ideal é um estado da matéria em que a interação das partículas é desprezível, a energia potencial de interação tende a zero. Apenas a energia do movimento, que depende da velocidade das partículas, pode ser considerada significativa.
Pressão de gás ideal
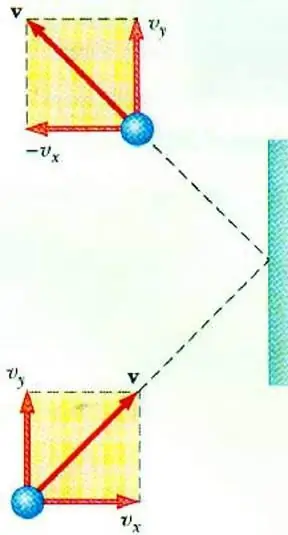
Revelar a relação entre a pressão do gás e a velocidade de suas partículas permite a equação básica do MKT de um gás ideal. Uma partícula em movimento em um recipiente, ao colidir com a parede, transfere para ela um impulso, cujo valor pode ser determinado com base na segunda leiNewton:
F∆t=2m0vx
A mudança no momento de uma partícula durante o impacto elástico está associada a uma mudança na componente horizontal de sua velocidade. F é a força que atua do lado da partícula na parede por um curto período de tempo t; m0 - massa da partícula.
Todas as partículas de gás colidem com a superfície de área S durante o tempo ∆t, movendo-se na direção da superfície com velocidade vx e localizadas em um cilindro de volume Sυ x Δt. Na concentração de partículas n, exatamente metade das moléculas se move em direção à parede, a outra metade se move na direção oposta.
Tendo considerado a colisão de todas as partículas, podemos escrever a lei de Newton para a força que atua na área:
F∆t=nm0vx2S∆t
Como a pressão do gás é definida como a razão entre a força que atua perpendicularmente à superfície e a área desta, podemos escrever:
p=F: S=nm0vx2
A relação resultante como equação básica do MKT não pode descrever todo o sistema, pois apenas uma direção de movimento é considerada.
Distribuição Maxwell
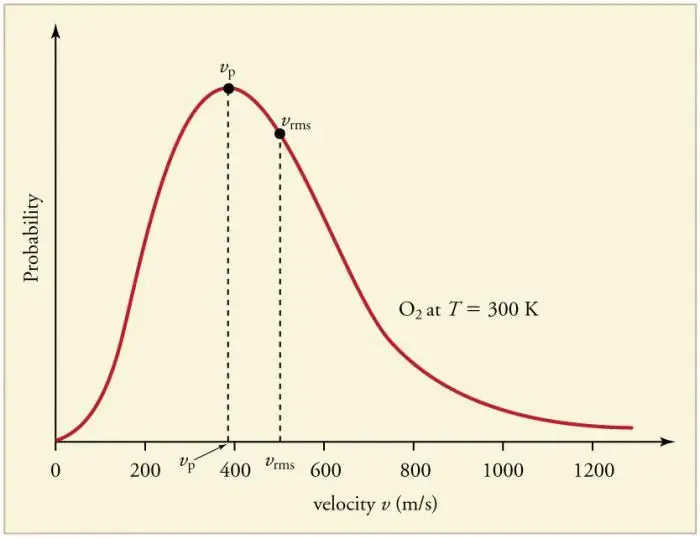
Contínuas e frequentes colisões de partículas de gás com as paredes e entre si levam ao estabelecimento de uma certa distribuição estatística das partículas em termos de velocidades (energias). As direções de todos os vetores de velocidade são igualmente prováveis. Essa distribuição é chamada de distribuição de Maxwell. Em 1860 esse padrão foiderivado por J. Maxwell com base no MKT. Os principais parâmetros da lei de distribuição são chamados de velocidades: provável, correspondente ao valor máximo da curva, e raiz quadrada média vkv=√‹v2 › - o quadrado médio da velocidade da partícula.
O aumento da temperatura do gás corresponde ao aumento da velocidade.
Com base no fato de que todas as velocidades são iguais, e seus módulos têm o mesmo valor, podemos supor:
‹v2›=‹vx2› + ‹v y2› + ‹vz2›, de: ‹ vx2›=‹v2›: 3
A equação básica do MKT, levando em consideração o valor médio da pressão do gás, é:
p=nm0‹v2›: 3.
Esta relação é única na medida em que determina a relação entre os parâmetros microscópicos: velocidade, massa de partículas, concentração de partículas e pressão do gás em geral.
Usando o conceito de energia cinética das partículas, a equação básica do MKT pode ser reescrita de forma diferente:
p=2nm0‹v2›: 6=2n‹Ek›: 3
A pressão de um gás é proporcional ao valor médio da energia cinética de suas partículas.
Temperatura
Curiosamente, para uma quantidade constante de gás em um recipiente fechado, pode-se relacionar a pressão do gás e o valor médio da energia de movimento da partícula. Neste caso, a pressão pode ser medida medindo a energiapartículas.
O que fazer? Que valor pode ser comparado com a energia cinética? A temperatura acaba sendo esse valor.

Temperatura é uma medida do estado térmico das substâncias. Para medi-lo, é usado um termômetro, cuja base é a expansão térmica do fluido de trabalho (álcool, mercúrio) quando aquecido. A escala do termômetro é criada experimentalmente. Normalmente, são colocadas nele marcas correspondentes à posição do fluido de trabalho durante algum processo físico que ocorre em estado térmico constante (água fervente, gelo derretido). Termômetros diferentes têm escalas diferentes. Por exemplo, Celsius, Fahrenheit.

Escala de temperatura universal
Os termômetros a gás podem ser considerados mais interessantes em termos de independência das propriedades do fluido de trabalho. Sua escala não depende do tipo de gás utilizado. Em tal dispositivo, pode-se hipoteticamente destacar a temperatura na qual a pressão do gás tende a zero. Os cálculos mostram que esse valor corresponde a -273,15 oC. A escala de temperatura (escala de temperatura absoluta ou escala Kelvin) foi introduzida em 1848. A possível temperatura de pressão de gás zero foi tomada como o ponto principal desta escala. Um segmento unitário da escala é igual a um valor unitário da escala Celsius. Parece mais conveniente escrever a equação básica do MKT usando temperatura ao estudar processos de gás.
Relação entre pressão e temperatura
Empiricamente, você pode verificar queproporcionalidade da pressão do gás à sua temperatura. Ao mesmo tempo, verificou-se que a pressão é diretamente proporcional à concentração de partículas:
P=nkT,
onde T é a temperatura absoluta, k é uma constante igual a 1,38•10-23J/K.
O valor fundamental, que tem um valor constante para todos os gases, é chamado de constante de Boltzmann.
Comparando a dependência da pressão com a temperatura e a equação básica dos gases MKT, podemos escrever:
‹Ek›=3kT: 2
O valor médio da energia cinética do movimento das moléculas do gás é proporcional à sua temperatura. Ou seja, a temperatura pode servir como medida da energia cinética do movimento das partículas.






